Jimy Ma's Zone
0%

寒武纪面试题

Posted on Edited on In ,

字符串匹配问题

题目

输入两个长度为n的字符串 P, Q, 定义 M(i,j,k)为 p (i), p (i+1),… … p(i+k-1) 与 q (j), q (j+1),… … q(j+k-1)之间不同的字符数量. 也就是说 M (i,j,k)为以下集合的元素数量:

给定一个整数 S, 找到一个最长的 L, 使得 M(i,j,L) $\leq$ S, 并且 i + L - 1 $\leq$ n, j + L -1 $\leq$ n.

python代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def M_str1_str2( str1, str2, L ):
    count_error = L
    for i in range( 0, L ):
        if str1[i] == str2[i]:
            count_error -= 1;
    return count_error;

def L_str1_str2( str1, str2, N, S ):
    # 定义的是比较的字符串的长度
    for i in range( N, 0, -1 ):
    # 定义的是选择字符串1中的起始位置( N长的字符串有 N - i + 1个长度为i的字符串)
        for j in range( 0, N - i + 1 ):
            #定义的是选择字符串2中的起始位置
            for k in range( 0, N -i + 1 ):
                #如果找到了满足条件的,就输出,找不到就不输出了~~并在最后输出0
                if M_str1_str2( str1[j:j+i], str2[ k: k + i ], i ) <= S:
                    return i
    return 0

P = ""
Q = ""
N = int( input("大小:") )
P = input( "str1(size_str1 = %d):\n" %N )
Q = input("str2:\n")
S = int( input("门限:") )
L = L_str1_str2( P, Q, N, S )
print(L)

解题技巧

L_str1_str2 函数

输入: 两个字符串str1和str2
输出: 最大匹配长度

Step1: 字符串的长度(i)从N到1遍历
Stpe2: 字符串1的起始位置(j)从0到N-i遍历
Step3: 字符串2的起始位置(k)从0到N-i遍历
Step4: M不超过错误门限的相互匹配的字符串,如果能,则返回该长度. 若不能, 则回到Step1.
Step5: 如果没有找到匹配的字符串, 则返回的长度为0.

M_str1_str2函数

输入: 两个字符串段
输出: 两个字符串段的不匹配字符的个数

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int M_str1_str2( char* str1, char* str2, int size_str )
{
    int count_error = size_str;
    for( int i = 0 ; i < size_str ; i++ )
    {
        if( str1[i] == str2[i] )
            count_error -= 1;
    }
    return count_error;
}

int L_str1_str2( char* str1, char* str2, int size_str, int threshold )
{
    for( int i = size_str; i > 0; i-- ) //字符串比较部分的长度
    {
        for( int j = 0; j < size_str - i + 1; j++ ) //选择字符串1的起始位置
        {
            for( int k = 0; k < size_str - i + 1; k++) //选择字符串2的起始位置
            {
                if( M_str1_str2( &str1[j], &str2[k] , i ) <= threshold ) //说明找到了则返回S
                {
                    for( int l = j; l < j + i ; l++ )
                        cout << " *" << str1[l] << "* ";

                    cout << " match ";

                    for( int l = k; l < k + i ; l++ )
                        cout << " *" << str2[l] << "* ";

                    return i;
                }
            }
        }
    }
    return 0;   //如果没有找到则返回0即可
}
int main()
{
    int size_str;
    int threshold;
    char str1[100];
    char str2[100];
    printf("Please input the size of str:\n");
    scanf("%d",&size_str);
    printf("Please input the threshold:\n");
    scanf("%d",&threshold);
    printf("Please input str1\n");
    scanf("%s",str1);
    printf("Please input str2\n");
    scanf("%s",str2);
    printf( "\n%d", L_str1_str2(str1,str2,size_str,threshold) );
    return 0;
}

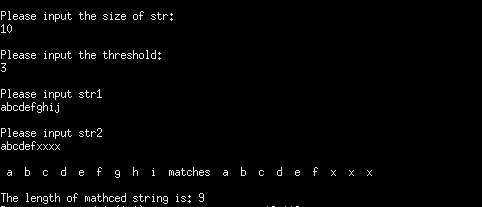
测试结果

测试的结果为:
测试结果

其中的输入的字符串的长度为 10(可任意大于等于0的数), 容忍的门限为3(可任意大于等于0的数).
可以看到匹配的字符串如上图所示,
而匹配的字符串长度为9.

图的深度遍历的问题

题目

这是一个经典的问题, 给定邻接矩阵e[N][N], 给定node1,node2节点, 通过深度搜索遍历,判断node1和node2是否连接.

流程

Step 1: 定义 visited 向量存储遍历过的节点.
Step 2: 给定Node1, Node2. 令Node1节点为当前的节点.
Step 3: 如果该节点不在visited中, 则将该节点存储至visited向量中.
Step 4: 依次从0到N遍历(i)图中的节点, 找到第i个不在visited中且可达的节点.
Step 5: 判断该节点是否为 Node2, 若为 Node2, 则搜索结束
Step 6: 若该节点不为Node2且尚有未达节点,则返回第三步
Step 7: 如果遍历了所有可达节点依然没有找到 Node2, 则输出 Node2 不可达.

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<iostream>
#include<vector>
#include <algorithm>
using namespace std;
vector<int> visited = {};
bool find_visited( vector<int> visited, int node )
{
    int size_visited = visited.size();
    for( int i = 0; i < size_visited; i++ )
    {
        if( visited[i] == node )
        {
            return true;
        }
    }
    return false;
}
void DFS( bool e[5][5], int size_graph, int node1, int node2 )
{
    if(!find_visited(visited,node1))
    {
        visited.push_back(node1);
        cout << node1;
    }
    for( int i = 0; i < size_graph; i++ )
    {
        if( !find_visited( visited, i ) && e[node1][i] )
        {
            visited.push_back(i);
            cout << i;
            if( i==node2 )
            {
                printf( "\n" );
                return;
            }
            DFS(e,size_graph,i,node2);
        }
    }
}
int main()
{
    vector<int> a = {};
    bool e[5][5] ={ { 0,1,1,0,0 },
                    { 1,0,1,0,1 },
                    { 1,1,0,0,0 },
                    { 0,1,1,0,1 },
                    { 0,1,1,0,0 } };
    int size_graph = 5;
    for( int i = 0; i < 5; i++ )
    {
        for( int j = 0; j < 5; j++ )
            printf("%d",e[i][j]);
        printf("\n");
    }

    printf("please input node1 ( 0--%d )\n",size_graph-1);
    int node1;
    cin >> node1;


    printf("please input node2( 0--%d )\n",size_graph-1);
    int node2;
    cin >> node2;

    DFS(e,5,node1,node2);
    if( find_visited( visited, node2 ) )
    {
        printf("node1 can get to node2");
    }
    else
        printf("node1 cannot get to node2");
    return 0;
}

测试结果

测试结果为:
测试结果

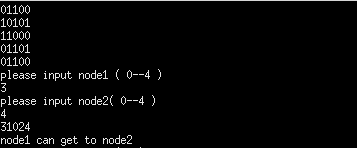
测试的邻接矩阵为:

图形化表达为:

有向图

从节点3出发, 找到节点4.
可以看到深度搜索的顺序为3->1->0->2->4,可以看到输出搜索成功.

测试结果

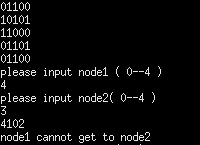
从节点4出发,找到节点3. 可以看到深度搜索的顺序为4->1->0->2, 可以看到输出搜索失败.