超密集组网建模
针对场景
- 基站
- 随机分布 / 均匀分布
- 用户
- 随机分布 / 均匀分布
- $n_{\mathsf{bs}} < n_{\mathsf{ue}}$
两种情况
Case 1
- 固定用户数,固定基站数
Problem 1
- 统计基站的服务范围内大概有多少个用户?
Problem 2
- 大概需要多少的带宽?
Case 2
- 固定基站数,不固定用户数
Problem
- 能服务的用户数
主要问题
- 资源分配问题
分配的资源
- 频带
- 功率
涉及到的问题
- 复用问题
- 用户需求的多样性
- 不同频段的聚合
Case1 - Problem1 分析
- 随机分布的用户,随机分布的基站,固定用户数,固定基站数,统计基站的服务范围内大概有多少个用户。
区域的参数汇总如下表:
| 参数 | 数值 |
|---|---|
| 基站数 | 200 |
| 用户数 | 1000 |
| 区域面积 | 100$\times$100 |
基站的分布情况的示意图
根据上面的参数,我们就能勾画出基站的分布情况的示意图。基站的示意图如下图所示:
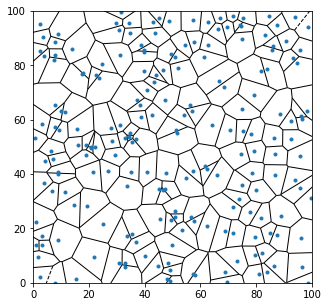
用户的分布情况示意图
由于用户也是随机分布的,我们也可以画出用户的分布情况的示意图。如下图所示。
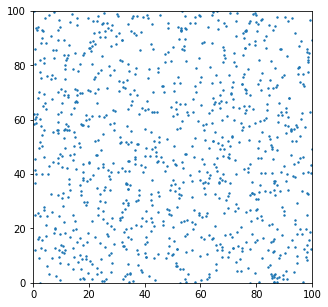
用户均匀的分布在整个区域的周围。
每个基站大概需要服务多少个用户?
有了基站的统计分布规律,有了基站的统计分布规律,我们就可以去讨论基站服务的用户数这个统计规律了。首先我们通过画图的方法,对这件事情有一个直观的认识:
我们把不同的基站的服务区域用泰森多边形去区分它,然后我们去观察每个泰森多边形里面到底有多少个用户,示意图如下,其中不同基站所服务的用户尽量用不同的颜色去表示(目前阶段为了简单,相邻不同区域的用户的颜色可能一样)。
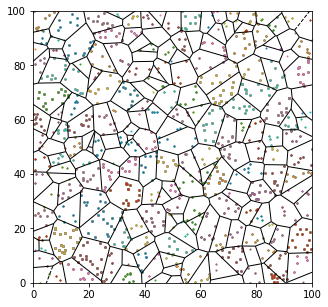
为了有一个直观的认识,我们可以观察这250个基站,去统计基站服务用户数的直方图。
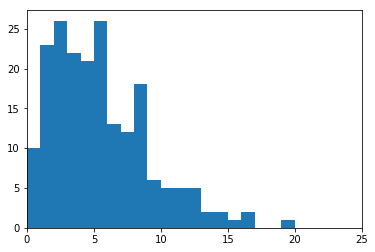
点数太少了,统计特性出不来,解决的办法是进行更多次的仿真,画图,给出更准确的统计特性。
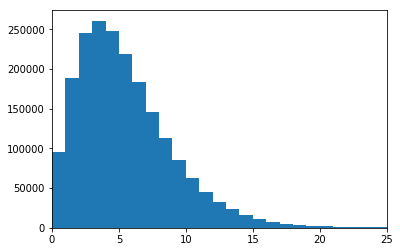
很好,统计特性出来了。
看起来像是一个高斯分布的离散情况。离散情况下能逼近高斯分布的也就只有二项分布和泊松分布了。
在进一步推断之前,首先把频率分布直方图进行归一化。
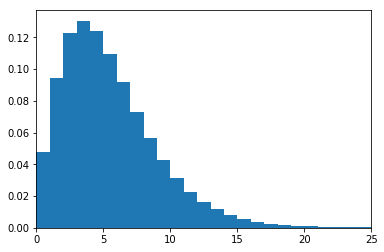
我们将上述的频率分布直方图,用$\mathcal{B}(1000,1 / 200)$拟合一下试试。其中$\mathcal{B}$表示二项分布,看看能不能拟合上。
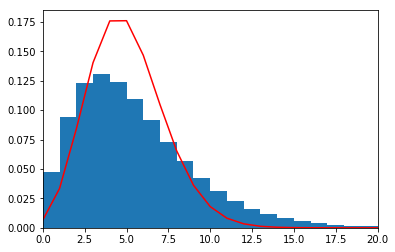
看来拟合不上思密达。
下一步将考虑如何对该问题进行数学上的推导。
单个基站下服务用户个数的统计分布规律
因为用户是随机分布的,因此在单位面积上的用户数其实是相等的,所以单个基站上有服务了多少个用户,其实可以考虑该基站的服务区域的面积。用该面积乘以用户的密度就可以求出服务的总数了。
换句话说,如果想知道单个基站下服务用户的概率质量分布函数,也只需要知道服务区域的面积就行了。因为整个小区中用户的数量已知,密度就已知了。单个基站的服务用户数的统计分布规律服从泊松分布。
将上述陈述可以总结成两个命题如下:
命题一: 在Case1的情况下,对于小区中的单个小基站而言,如果知道该小基站的服务面积为$\sigma$,用户的密度为$\lambda_{\mathsf{ue}}$,那么该小基站的服务用户数$\bar{n}$的统计平均值为:
命题二: 在Case1的情况下,对于小区中的单个小基站而言,如果知道该小基站的服务面积为$\sigma$,用户的密度为$\lambda_{\mathsf{ue}}$,那么该小基站的服务用户数$n$的概率质量分布函数为: